Thanksgiving week, time to relax and play some games. While I’m not playing Fallout 4, I’ve still got something open!
Cross Set is a recent release on Steam, with a premise similar to Sudoku. These games are always good to relax with, because you can usually go through the mechanical motions to solve them and let your brain idle. The rules for this puzzler are simple:
- There is an NxN square grid (up to 9x9)
- The winning solution is to have every row and column containing every number 1 through N
- The grid is already constrained by sets of numbers included in each cell
- As a helping tool, cells can be locked in place
The Premise
If you’ve ever played sudoku, the game should look familiar. This is roughly the intermediate stage of solving a sudoku puzzle. I quickly got bored after I cleared the first two levels, but still had the urge to 100% complete the puzzles. Briefly, I considered refunding my purchase if I could write a solver for the game. Then I figured if I wrote the solver, then there’s no point in requesting a refund, as I clearly got my money’s worth. Sounds like a fun programming challenge, so let’s get started! (I also considered writing a tool to help with the two incremental games I open occasionally, but interacting with them wasn’t as simple.)
Input
For each level, the grid can easily be serialized into a text format, delimiting each cell with a space and each row with a newline. From there, it will be parsed into a PuzzleGrid object.
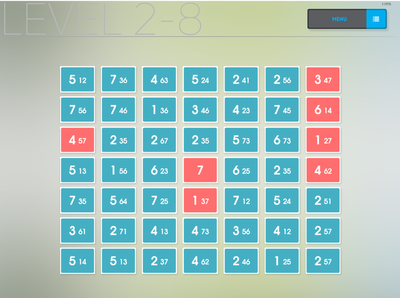
2-8.txt:
512 736 463 524 241 256 347
756 746 136 346 423 745 614
457 235 267 235 573 673 127
513 156 623 7 625 235 462
735 564 725 137 712 524 251
361 271 413 473 356 412 257
514 513 237 462 246 125 257
Output
The script should print out a solved grid that I can then manually enter into the game. Not great, but much easier than interacting with Tap Tap Infinity or Time Clickers.
Purpose
Ideally, the script should solve the grid completely. However, I’m not sure if my approach to solving the puzzle will be able to work 100% of the time. If the puzzle can’t actually be solved, I’d like the program to at least return a partially solved puzzle. Absolute worst case is no cells solved, so I probably need to attempt solving it by hand and figure out a new algorithm.
Scaffolding
Folder Structure
main.py
cross_set/
__init__.py
solver.py - Contains the algorithms
puzzle_grid.py - Contains the objects detailing the puzzle
Reading Input
Simple enough, I want to read cells from a text file. This will be in main.py, so that the cross_set package only needs to deal with one kind of input. I’ll go ahead and define that to be a list of list of sets. If in the future I want to change input methods (maybe a fancy curses TUI?), then I just change main.py .
main.py
import sys
import cross_set
# Script must be run directly, not imported
if __name__ == '__main__':
# Script requires one argument: filename
if len(sys.argv) < 2:
print("Filename argument required")
sys.exit(1)
# Filename is the first argument (sys.argv[0] is the program name)
filename = sys.argv[1]
# Read from the provided filename, assuming it exists
puzzle_contents = ""
with open(filename) as puzzle_file:
puzzle_contents = puzzle_file.read()
# Stuff the contents into puzzle (list of list of sets) with minimal validation
puzzle = []
# Each line: Add a list to puzzle
for line in puzzle_contents.split('\n'):
puzzle_line = []
# Each cell: Add a set to puzzle_line
for cell in line.split(' '):
# Discard spaces used for alignment
if cell == '':
continue
# Each number: Convert to an int before adding to the set
cell_numbers = (int(x) for x in cell)
puzzle_line.append(set(cell_numbers))
puzzle.append(puzzle_line)
puzzle_grid = cross_set.PuzzleGrid(puzzle)
solved_grid = cross_set.solve(puzzle_grid)
print(solved_grid)Puzzle Objects
The main object will be the PuzzleGrid, representing the grid of cells, with coordinates 0,0 at the top left corner. There are several methods to implement here that I think would be useful for writing the solving algorithms:
__init__(puzzle)- Takes alist of list of setsrepresenting the grid__str__()- Returns a nice serialized version of the grid (which should be equivalent format to what is passed in from the file)column(x)- Returns a list of cells in Column xrow(y)- Returns a list of cells in Row ycell(x,y)- Get the cell located at Column x, Row yset_cell(x,y,val)- Set the cell located at Column x, Row ysize()- How big is the puzzle?- equality operators - Are these two puzzles identical?
puzzle_grid.py
import copy
import itertools
class PuzzleGrid(object)
def __init__(self, puzzle):
# Check that the provided grid is square
num_rows = len(puzzle)
for row in puzzle:
if len(row) != num_rows:
raise ValueError("Puzzle grid is not square")
self.grid = copy.deepcopy(puzzle)
def __str__(self):
# Get the size of the largest set in the puzzle
all_cells = (self.cell(x,y) for x,y in itertools.product(range(self.size()), range(self.size())))
padding = max(len(cell) for cell in all_cells)
rows = []
for row in self.grid:
cells = []
for cell in row:
# Print set(1,2,3) as 123, padding to the largest set in the puzzle
format_str = "%% %ds" % padding
compact_set = "".join(str(num) for num in cell)
cells.append(format_str % compact_set)
rows.append(" ".join(cells))
return "\n".join(rows)
def column(self, x):
return (row[x] for row in self.grid)
def row(self, y):
return self.grid[y]
def cell(self, x, y):
return self.grid[y][x]
def set_cell(self, x, y, val):
self.grid[y][x] = val
def size(self):
return len(self.grid)
def __eq__(self, other):
return self.grid == other.grid
def __ne__(self, other):
return not (self == other)Creating the Puzzle Object
At the end of main.py
puzzle_grid = cross_set.PuzzleGrid(puzzle)Solving and Printing Output
Simple process of running the solving algorithm and then printing the solved PuzzleGrid
At the end of main.py
cross_set.solve(puzzle_grid)
print(puzzle_grid)Algorithm Scaffolding
Standalone functions I can see use for in the algorithm:
- cell_solved(cell) - Returns whether the cell is solved
- column_solved(col) - Returns whether the column is completely solved
- row_solved(row) - Returns whether the row is completely solved
- puzzle_solved(puzzle) - Returns whether the puzzle is completely solved
solver.py
from cross_set.puzzle_grid import PuzzleGrid
def cell_solved(cell):
return len(cell) == 1
def list_solved(cell_list):
# All cells have one value
num_solved = sum(1 for cell in cell_list if cell_solved(cell))
if num_solved < len(cell_list):
return False
# There are no duplicate cells
cell_set = set(list(cell)[0] for cell in cell_list)
if len(cell_set) < len(cell_list):
return False
return True
column_solved = list_solved
row_solved = list_solved
def puzzle_solved(puzzle):
for row_num in range(puzzle.size()):
if not row_solved(list(puzzle.row(row_num))):
return False
for col_num in range(puzzle.size()):
if not column_solved(list(puzzle.column(col_num))):
return False
return True
def solve(puzzle):
return PuzzleGrid(puzzle.grid)First Attempt
My first step when solving a puzzle by hand is to mentally cross off any numbers contradict already locked numbers. This is a good starting point for the solver, so let’s see how far it gets me. I want to keep running this on the puzzle until there are no more changes to the grid (hopefully it’s solved at that point).
solver.py
# Remove invalidated cell values, this is the most basic thing to do to a puzzle
def weed(puzzle):
old_puzzle = puzzle
puzzle = PuzzleGrid(puzzle.grid)
for row, column in itertools.product(range(puzzle.size()), range(puzzle.size())):
cell = old_puzzle.cell(column, row)
if cell_solved(cell):
(locked_value,) = cell
# Get a list of cells in the same row and column to weed
in_row = ((c, row) for c in range(puzzle.size()) if not c == column)
in_column = ((column, r) for r in range(puzzle.size()) if not r == row)
cells_to_check = itertools.chain(in_row, in_column)
# Read cells from the puzzle being modified and remove the locked value if it exists, saving off to the new puzzle
for x,y in cells_to_check:
other_cell = puzzle.cell(x, y)
if locked_value in other_cell:
other_cell.remove(locked_value)
return puzzle
def solve(puzzle):
weeded_puzzle = weed(puzzle)
while weeded_puzzle != puzzle:
puzzle = weeded_puzzle
weeded_puzzle = weed(puzzle)
return puzzleAs it turns out, only one iteration of the algorithm is performed before it’s useless!
125 367 346 245 124 256 347
567 467 136 346 234 457 146
457 235 267 235 357 367 127
135 156 236 7 256 235 246
357 456 257 13 127 245 125
136 127 134 34 356 124 257
145 135 237 246 246 125 257
This is useful to define a minimal form of the puzzle though, so let’s make that a helper function.
solver.py
def minimal_form(puzzle):
weeded_puzzle = weed(puzzle)
while weeded_puzzle != puzzle:
puzzle, weeded_puzzle = weeded_puzzle, weed(puzzle)
return weeded_puzzleSecond Attempt
The next method I use mentally is to look for the cells that contain the only instance of a value in a row/column. That cell can then be finalized to that single value.
solver.py
# TODO: Get singles from old_puzzle, update them on puzzle
def lock_singles(puzzle):
old_puzzle = puzzle
puzzle = minimal_form(puzzle)
rows = (puzzle.row(row) for row in range(puzzle.size()))
columns = (puzzle.column(column) for column in range(puzzle.size()))
# Take advantage of the fact these are all references and discard WHAT they are
cell_lists = itertools.chain(rows, columns)
for cell_list in cell_lists:
values = []
for cell in cell_list:
values.extend(list(cell))
singles = (i for i in range(1, puzzle.size()+1) if values.count(i) == 1)
for single in singles:
for cell in cell_list:
if single in cell:
# Don't update already locked cells
if len(cell) > 1:
cell.intersection_update({single})
# It's a single for a reason, don't need to check the rest of the cells once it's found
continue
return puzzle
def solve(puzzle):
solved_puzzle = puzzle
# Loop until there's no improvement
while True:
solved_puzzle = minimal_form(puzzle)
solved_puzzle = lock_singles(solved_puzzle)
if puzzle == solved_puzzle:
break
else:
puzzle = solved_puzzle
return solved_puzzleNot the most functional approach, Python is starting to annoy me about now, but I’m not trying to make a masterpiece the first time through!
11 iterations later, and Level 2-8 was solved.
2 7 4 5 1 6 3
7 4 1 3 2 5 6
4 5 6 2 3 7 1
5 1 2 7 6 3 4
3 6 5 1 7 4 2
6 2 3 4 5 1 7
1 3 7 6 4 2 5
Here are the results after each iteration:
Iteration 1
125 367 346 245 124 256 347
567 467 136 346 2 457 146
4 235 267 235 357 367 1
135 156 236 7 256 235 4
357 6 257 13 127 245 125
136 127 134 34 356 124 257
145 135 237 246 246 125 257
Iteration 2
125 37 346 245 14 256 37
57 47 1 34 2 457 6
4 235 267 235 357 367 1
135 15 236 7 56 235 4
357 6 257 13 17 4 25
136 127 134 34 356 124 257
15 135 237 246 46 125 257
Iteration 3
125 37 346 245 14 256 37
57 47 1 3 2 57 6
4 235 267 235 357 367 1
135 15 236 7 56 235 4
357 6 257 13 17 4 25
136 127 34 34 356 12 257
15 135 237 246 46 125 257
Iteration 4
125 37 346 25 14 256 37
57 4 1 3 2 57 6
4 235 267 25 357 367 1
135 15 236 7 56 235 4
3 6 257 1 7 4 25
136 127 3 4 356 12 257
15 135 237 26 4 125 257
Iteration 5
25 37 4 25 1 256 37
57 4 1 3 2 57 6
4 235 267 25 35 367 1
15 15 26 7 56 3 4
3 6 25 1 7 4 25
16 127 3 4 56 12 257
15 3 27 6 4 125 257
Iteration 6
25 7 4 25 1 6 3
57 4 1 3 2 57 6
4 25 267 25 3 67 1
15 15 2 7 56 3 4
3 6 25 1 7 4 25
16 12 3 4 56 12 7
15 3 27 6 4 125 257
Iteration 7
25 7 4 25 1 6 3
7 4 1 3 2 5 6
4 25 6 25 3 7 1
15 15 2 7 6 3 4
3 6 5 1 7 4 2
16 12 3 4 5 12 7
15 3 7 6 4 125 25
Iteration 8
25 7 4 25 1 6 3
7 4 1 3 2 5 6
4 25 6 25 3 7 1
15 15 2 7 6 3 4
3 6 5 1 7 4 2
6 12 3 4 5 12 7
1 3 7 6 4 2 5
Iteration 9
2 7 4 5 1 6 3
7 4 1 3 2 5 6
4 25 6 25 3 7 1
5 1 2 7 6 3 4
3 6 5 1 7 4 2
6 2 3 4 5 1 7
1 3 7 6 4 2 5
Iteration 10
2 7 4 5 1 6 3
7 4 1 3 2 5 6
4 5 6 2 3 7 1
5 1 2 7 6 3 4
3 6 5 1 7 4 2
6 2 3 4 5 1 7
1 3 7 6 4 2 5
Iteration 11
2 7 4 5 1 6 3
7 4 1 3 2 5 6
4 5 6 2 3 7 1
5 1 2 7 6 3 4
3 6 5 1 7 4 2
6 2 3 4 5 1 7
1 3 7 6 4 2 5
This solves several puzzles up until Level 3-4:
512 534 352 123 53
125 235 1345 125 42
45 53 312 241 412
1234 134 3452 23 24
453 423 1245 4523 4512
Three iterations run before it bails, leaving me with:
125 4 23 123 35
125 235 134 125 24
45 35 123 124 124
1234 13 5 23 24
345 23 124 2345 1245
Third Attempt
Inspecting the output, I see some patterns… The rightmost column contains two cells with {2,4}! Since only those two cells can contain 2 and 4, I can remove that option from other cells in the column. In general, if N cells hold the exact same N-tuple of numbers, then you can exclude those numbers from any other cell in their row/column, because those N cells are the only ones that could contain those numbers.
def ntuple_equals(puzzle):
old_puzzle = puzzle
puzzle = minimal_form(puzzle)
rows = (puzzle.row(row) for row in range(puzzle.size()))
columns = (puzzle.column(column) for column in range(puzzle.size()))
# Take advantage of the fact these are all references and discard WHAT they are
cell_lists = itertools.chain(rows, columns)
for cell_list in cell_lists:
cell_list = list(cell_list)
ntuples = []
for cell in cell_list:
if cell_list.count(cell) == len(cell) and cell not in ntuples:
ntuples.append(cell)
for tuple in ntuples:
for cell in cell_list:
if cell != tuple:
# Remove any elements from the tuple from cell
cell.difference_update(tuple)
return puzzle
def solve(puzzle):
solved_puzzle = puzzle
# Loop until there's no improvement
while True:
solved_puzzle = minimal_form(puzzle)
solved_puzzle = lock_singles(solved_puzzle)
solved_puzzle = ntuple_equals(solved_puzzle)
if puzzle == solved_puzzle:
break
else:
puzzle = solved_puzzle
return solved_puzzleFantastic! This solves Level 3-4 with ease in 4 iterations!
Iteration 1
125 4 23 123 35
125 235 134 125 24
45 35 123 124 1
1234 13 5 23 24
345 23 124 2345 15
Iteration 2
5 4 2 1 3
12 235 34 5 24
4 35 3 2 1
123 13 5 3 24
3 23 1 34 5
Iteration 3
5 4 2 1 3
1 3 4 5 2
4 5 3 2 1
2 1 5 3 4
3 2 1 4 5
Iteration 4
5 4 2 1 3
1 3 4 5 2
4 5 3 2 1
2 1 5 3 4
3 2 1 4 5
Between iterations 1 and 2, the right column is stripped of any instances of 2 or 4 that aren’t in rows 2 and 4 (heh?). Works as intended! Let’s see how far this goes.
…
…
All the way to Level 4-5 before it gets stumped:
612 563 513 534 62 462
245 12 462 24 623 261
534 562 23 235 16 145
612 13 456 245 45 241
25 463 645 13 16 43
35 251 341 126 45 613
This is the final output:
16 56 13 345 2 46
5 12 246 24 3 126
4 256 23 235 16 15
16 3 46 245 45 124
2 46 5 13 16 34
3 125 14 126 45 16
If I help the solver along, by removing the 1 from cell 5,5 then it can solve the puzzle, but I’m not sure where to find the algorithm hidden here. Looks like the journey is about to be over. Oh, but hold on now, the far right column only has a single 5 in row 3. Why isn’t it getting locked by the second algorithm? Aha, when I iterate over cell_list twice, the second time it’s not actually iterating. This is due to iterating over a python generator produced by itertools.chain, which will act like it’s empty after I’ve iterated over it exactly once. Annoying, but the easy fix is cell_list = list(cell_list). Level 4-5 is solved now, so we’re back in business.
6 5 1 3 2 4
5 1 2 4 3 6
4 6 3 2 1 5
1 3 6 5 4 2
2 4 5 1 6 3
3 2 4 6 5 1
For Your Sanity
While typing in puzzles, I occasionally missed a digit, resulting in some odd looking solutions where some cells had no values! So, I added a sanity check for each iteration.
def sanity_check(puzzle):
for row, column in itertools.product(range(puzzle.size()), range(puzzle.size())):
cell = puzzle.cell(column, row)
if len(cell) == 0:
return False
return TrueFinal Thoughts
Only one puzzle left on level 8, this must be a doozy. Three iterations later:

In the end what did I get out of this?
- I realized how much I prefer C++ to Python. I think with the right set of types it would have been easier to express the algorithms. Although the itertools module was extremely handy, I’m not sure if I would be able to do the same things as easily in C++.
- I enjoyed the game, props to the developers, especially for addressing my feedback on the discussion forum by an update within a day.
- I learned to appreciate the ten key typing lessons I had in highschool.
- I worked my brain by trying to memorize sequences as I manually entered them back into the game.
- I wondered… the puzzles seem weak, most only requiring one to three iterations. Perhaps this is the power of the algorithm? Flaw of the game design?
I’d appreciate feedback on the code, which can be found on Github! Especially anything that makes the algorithms more readable.